Sword to Offer-12 矩阵中的路径 ❀❀❀

30 Mar 2020 in Algorithm

• 题目描述：请设计一个函数，用来判断在一个矩阵中是否存在一条包含某字符串所有字符的路径。路径可以从矩阵中的任意一个格子开始，每一步可以在矩阵中向左，向右，向上，向下移动一个格子。如果一条路径经过了矩阵中的某一个格子，则该路径不能再进入该格子。

• 例如
  矩阵中包含一条字符串"bcced"的路径，但是矩阵中不包含"abcb"路径，因为字符串的第一个字符b占据了矩阵中的第一行第二个格子之后，路径不能再次进入该格子。

解题思路：

回溯法
1、暴力搜索整个矩阵，以矩阵中每个点为起点开始回溯流程；
2、退出判真条件为找到点的个数等于str长度；
3、退出判假条件为：
（1）该点超出了矩阵范围；
（2）该点值不等于str下一个值；
（3）该点已经在本次搜寻流程中走过；
4、上面两步没有返回，说明该点满足搜寻条件，接下来：
（1）将该点的状态标记为已走过；
（2）递归搜寻，以其四个邻接的点为起点开始判断是否与str后面子串匹配，匹配则返回true；

注：邻接点会判断自身是否满足条件，再将问题抛给它满足条件的邻接点。
(a) 若有这样的路径，最后搜寻问题会被抛给最后一个匹配的点，在对比长度时返回，而调用它的 上一个点，上上个点…都会返回true，总问题返回true；
(b) 若不存在这样的路径，最终会走到最后两步，将第一个点状态置为false，并返回false。

5、上面都未返回，说明虽然该点满足条件，以它为起点并不能找到路径，回溯该点，将走过状态置为false，并返回false，开始以矩阵下一个点为起点寻找。

问题图解：

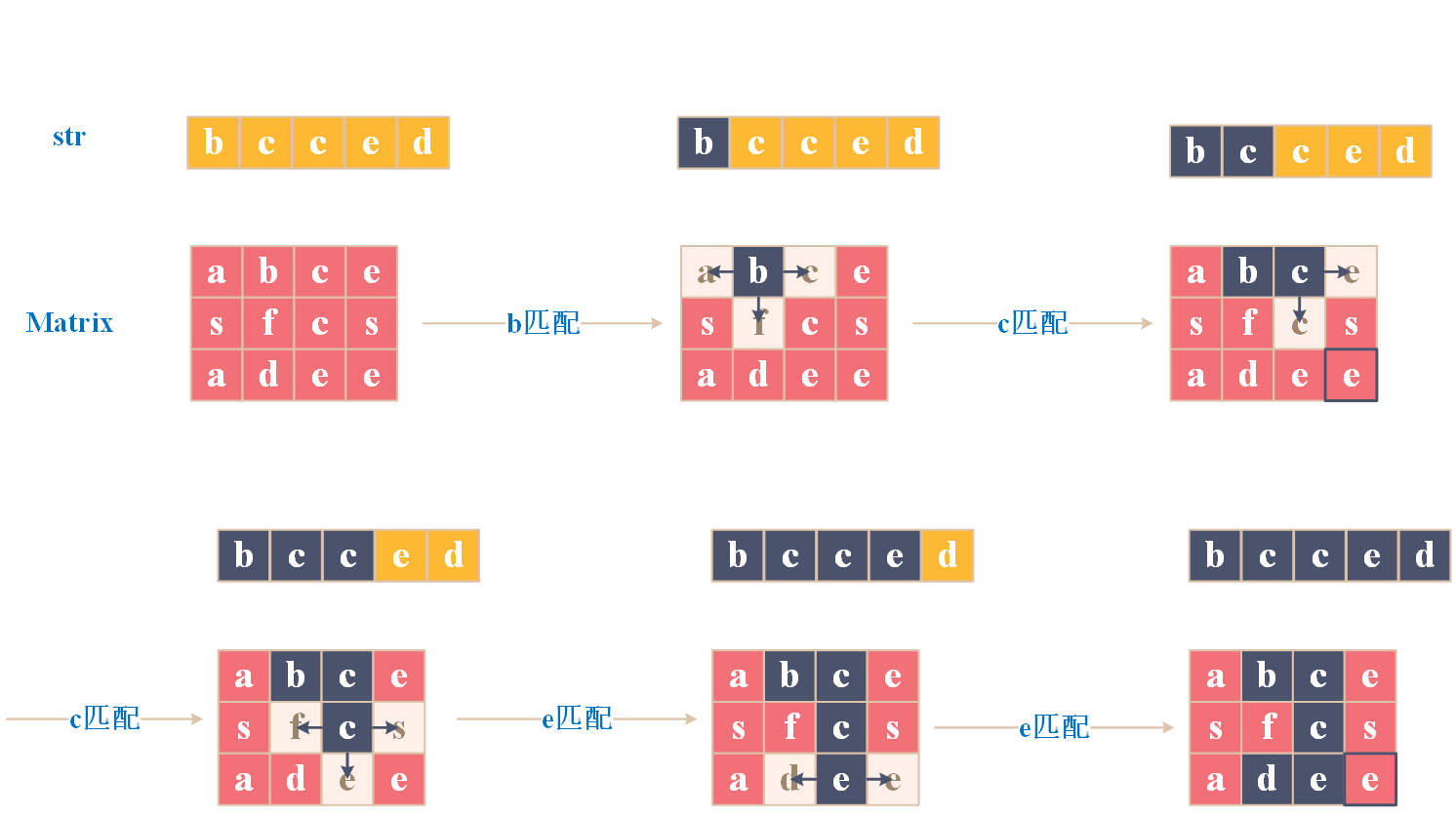
AC代码：

// Finding Path in Matrix

public class Solution {
    public boolean hasPath(char[] matrix, int rows, int cols, char[] str) {
        // turn matrix into a two-dimensional array
        char[][] searchMatrix = new char[rows][cols];
        for (int i=0; i<rows; i++) {
            for (int j=0; j<cols; j++) {
                searchMatrix[i][j] = matrix[i*cols+j];
            }
        }
        // create a mark matrix to sign the char has been selected or not
        boolean[][] status = new boolean[rows][cols];
        // searching,if traverse the whole matrix but cannot find,return false
        int position = 0; 
        //position means the element that has been selected
        for (int m=0; m<rows; m++) {
            for (int n=0; n<cols; n++) {
                if (backTracking(searchMatrix, status, rows, cols, m, n, str, position)) {
                    return true;
                }
            }
        }
        return false;
    }
    
    private boolean backTracking(char[][] matrix, boolean[][] status, int rows, int cols, 
                                             int i, int j, char[] str, int position) {
        // 找到的元素个数等于字符串长度时判断路径成功
        if (position == str.length)  { 
            return true;
        }
        // 不在矩阵范围内或已走过或不匹配
        if (i<0 || i>=rows || j<0 || j>=cols || status[i][j] || matrix[i][j]!=str[position]) {
            return false;
        }
        // 走到此处，说明该点匹配但是不是str最后一个点
        status[i][j] = true;
        // 寻找该点邻接的点是否能满足子路径
        if (backTracking(matrix, status, rows, cols, i-1, j, str, position+1)||
            backTracking(matrix, status, rows, cols, i+1, j, str, position+1)||
            backTracking(matrix, status, rows, cols, i, j-1, str, position+1)||
            backTracking(matrix, status, rows, cols, i, j+1, str, position+1)) {
            return true;
        }
        // 如果邻接的点无法找到子路径，回退该点
        status[i][j] = false;
        return false;
    }
}

补充说明：

• 这里是牛客编码链接