Sword to Offer-10.4 变态跳台阶 ❀

27 Mar 2020 in Algorithm

• 题目描述：一只青蛙一次可以跳上1级台阶，也可以跳上2级…它也可以跳上n 级。求该青蛙跳上一个n级的台阶总共有多少种跳法（先后次序不同算不同的结果）。

解题思路：

1、区别于上一个跳台阶问题（普通斐波那契问题）;
2、第一次可以跳1~n级; ，
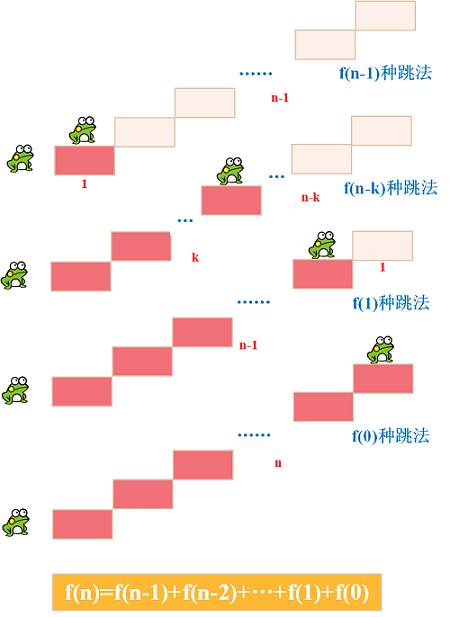
（1）假设第一次只跳1级，那么接下来是一个f(n-1)跳跃子问题；
（2）假设第一次跳k级，那么接下来是一个f(n-k)跳跃子问题；
（3）假设第一次跳n-1级，那么接下来是一个f(1)跳跃子问题，此时f(1)=1，因为第一次跳了n-1级，第二次只能跳一级，只有这种固定的可能；
（4）最后是第一次就跳了n级，此时为f(0)=1，一次跳完；
3、简化计算公式
（1）f(n)=f(n-1)+f(n-2)+…+f(1)+f(0)
（2）f(n-1)=f(n-2)+f(n-3)+…+f(1)+f(0)
（3）两式相减可得f(n)=2*f(n-1)
4、计算f(n)实际上只需要保存下f(n-1)的值，需要保留的值只有一个。

问题图解：

AC代码：

// Jump Stairs When Once 1~n Stairs

public class Solution {
    public int JumpFloorII(int target) {
        if (target <=2) {
            return target;
        }
        int pre = 2;
        int result = 0;
        for (int i=3; i<=target; i++) {
            result = 2 * pre;
            pre = result;
        }
        return result;
    }
}

补充说明：

• 这里是牛客编码链接