Sword to Offer-07 重建二叉树 ❀❀

21 Mar 2020 in Algorithm

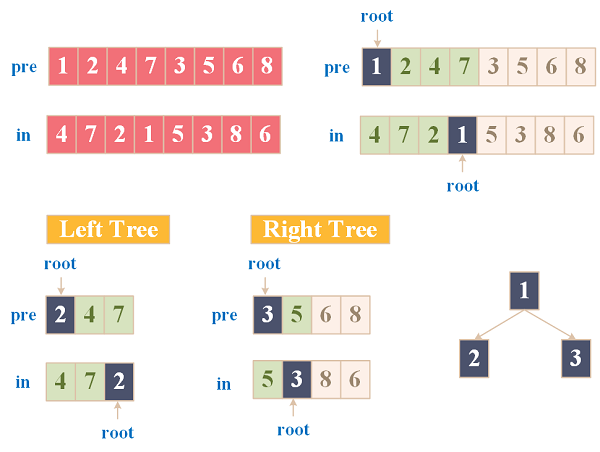
• 题目描述：输入某二叉树的前序遍历和中序遍历的结果，请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。

• 例如：输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6}，则重建二叉树并返回。

解题思路：

1、二叉树结构为串起来的TreeNode，每个TreeNode有一个值value和两个指针，指针left指向左孩子，right指向右孩子，构造完成后返回二叉树，即返回其root结点;
2、前序遍历：Root->Left->Right; 中序遍历：Left->Root->Right;
3、前序遍历开头的结点总能将中序遍历分为Left子树和Right子树两部分，根据划分后两部分的长度，又可以把前序遍历的Left子树和Right子树分开，就分别得到了两个子树的前序和中序遍历；
4、对已知前序和中序遍历的Left和Right子树，又可以重复上述步骤递归求解；
5、递归退出条件为子树长度为0。

问题图解：

AC代码：

// Construct Binary Tree using Pre-order and Mid-order Traversal

public class Solution {
    public TreeNode reConstructBinaryTree(int[] pre,int[] in) {
        // 为了不用每次重新构造pre和in数组，选择start和end指针进行切割，重载该方法
        TreeNode root = reConstructBinaryTree(pre, 0, pre.length-1, in, 0, 
                                                              in.length-1);
        return root;
    }
    
    // 递归调用自身用来划分左右子树
    private TreeNode reConstructBinaryTree(int[] pre, int preStart, int preEnd,
                                    int[] in, int inStart, int inEnd) {
        // 子树大小为0是递归终点
        if (preStart>preEnd || inStart>inEnd) {
            return null;
        }
        // 每次递归取前序的第一个值，必定为该子树的root
        TreeNode root = new TreeNode(pre[preStart]);
        // 在中序数组中找到root，并将其分为左右两部分，分别进行子树构造
        for (int i=inStart; i<=inEnd; i++) {
            if (in[i] == pre[preStart]) {
                root.left = reConstructBinaryTree(pre, preStart+1,
                                          preStart+i-inStart, in, inStart, i-1);
                root.right = reConstructBinaryTree(pre, preStart+i-inStart+1,
                                          preEnd, in, i+1, inEnd);
            }
        }
        return root;
    }
}

补充说明：

• 注意：难点在两个子树的划分，起点终点要算准确。
• 这里是牛客编码链接